Author: Ed Nelson
Department of Sociology M/S SS97
California State University, Fresno
Fresno, CA 93740
Email: ednelson@csufresno.edu
Note to the Instructor: This exercise uses the 2014 General Social Survey (GSS) and SDA to compare means and test hypotheses. SDA (Survey Documentation and Analysis) is an online statistical package written by the Survey Methods Program at UC Berkeley and is available without cost wherever one has an internet connection. The 2014 Cumulative Data File (1972 to 2014) is also available without cost by clicking here. For this exercise we will only be using the 2014 General Social Survey. A weight variable is automatically applied to the data set so it better represents the population from which the sample was selected. You have permission to use this exercise and to revise it to fit your needs. Please send a copy of any revision to the author. Included with this exercise (as separate files) are more detailed notes to the instructors and the exercise itself. Please contact the author for additional information.
I’m attaching the following files.
- Extended notes for instructors (MS Word; .docx format).
- This page (MS Word; .docx format).
Goals of Exercise
The goal of this exercise is to compare means and test hypotheses. The exercise also gives you practice in using MEANS in SDA.
Part I – Computing Means
Populations are the complete set of objects that we want to study. For example, a population might be all the individuals that live in the United States at a particular point in time. The U.S. does a complete enumeration of all individuals living in the United States every ten years (i.e., each year ending in a zero). We call this a census. Another example of a population is all the students in a particular school or all college students in your state. Populations are often large and it’s too costly and time consuming to carry out a complete enumeration. So what we do is to select a sample from the population where a sample is a subset of the population and then use the sample data to make an inference about the population.
A statistic describes a characteristic of a sample while a parameter describes a characteristic of a population. The mean age of a sample is a statistic while the mean age of the population is a parameter. We use statistics to make inferences about parameters. In other words, we use the mean age of the sample to make an inference about the mean age of the population. Notice that the mean age of the sample (our statistic) is known while the mean age of the population (our parameter) is usually unknown.
There are many different ways to select samples. Probability samples are samples in which every object in the population has a known, non-zero, chance of being in the sample (i.e., the probability of selection). This isn’t the case for non-probability samples. An example of a non-probability sample is an instant poll which you hear about on radio and television shows. A show might invite you to go to a website and answer a question such as whether you favor or oppose same-sex marriage. This is a purely volunteer sample and we have no idea of the probability of selection.
We’re going to use the General Social Survey (GSS) for this exercise. The GSS is a national probability sample of adults in the United States conducted by the National Opinion Research Center (NORC). The GSS started in 1972 and has been an annual or biannual survey ever since. For this exercise we’re going to use the 2014 GSS. To access the GSS cumulative data file in SDA format click here. The cumulative data file contains all the data from each GSS survey conducted from 1972 through 2014. We want to use only the data that was collected in 2014. To select out the 2014 data, enter year(2014) in the Selection Filter(s) box. Your screen should look like Figure 6-1. This tells SDA to select out the 2014 data from the cumulative file.
Notice that a weight variable has already been entered in the WEIGHT box. This will weight the data so the sample better represents the population from which the sample was selected. Notice also that in the SAMPLE DESIGN line SRS has been selected.
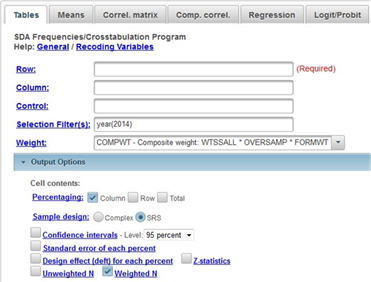
Figure 6-1
The GSS is an example of a social survey. The investigators selected a sample from the population of all adults in the United States. This particular survey was conducted in 2014 and is a relatively large sample of approximately 2,500 adults. In a survey we ask respondents questions and use their answers as data for our analysis. The answers to these questions are used as measures of various concepts. In the language of survey research these measures are typically referred to as variables. Often we want to describe respondents in terms of social characteristics such as marital status, education, and age. These are all variables in the GSS.
Let’s start by asking two questions.
- Do men and women differ in the number of years of school they have completed?
- Do men and women differ in the number of hours they worked in the last week?
Let’s start by getting the means for these variables. Click on MEANS in the menu bar at the top of SDA and enter the variables educ and hrs1 in the DEPENDENT box. The dependent variable will always be the variable for which you are going to compute means. Then enter the variable sex in the ROW box. This is the variable which defines the groups you want to compare. In our case we want to compare men and women. The output from SDA will show you the mean for the two dependent variables for both men and women. Notice that you must enter one or more variables in both the DEPENDENT and ROW boxes. That what it means when it says REQUIRED next to these boxes. Your screen should like Figure 6-2. Separate the variable names by either a space or a comma. Notice that the SELECTION FILTER(S) box and the WEIGHT box are both filled in. Click RUN THE TABLE to produce the means.
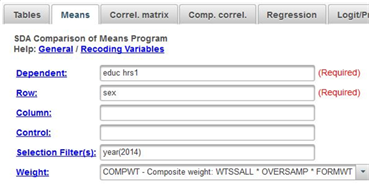
Figure 6-2
Men and women differ very little in the number of years of school they completed. Men have completed a little less than one-tenth of a year more than women. But men worked quite a bit more than women in the last week – a difference of a little more than five hours. By the way, only respondents who are employed are included in this calculation but both part-time and full-time employees are included.
Why can’t we just conclude that men and women have about the same education and that men work more than women? If we were just describing the sample, we could. But what we want to do is to make inferences about differences between men and women in the population. We have a sample of men and a sample of women and some amount of sampling error will always be present in both samples. The larger the sample, the less the sampling error and the smaller the sample, the more the sampling error. Because of this sampling error we need to make use of hypothesis testing.
Part II – Now it’s Your Turn
In this part of the exercise you want to compare men and women to answer these two questions.
- Do men and women differ in the number of hours per day they have to relax? This is variable hrsrelax in SDA.
- Do men and women differ in the number of hours per day they watch television? This is variable tvhours in SDA.
Use SDA to get the sample means and then compare them to begin answering these questions. Write a couple sentences describing the differences between men and women for both variables.
Part III – Hypothesis Testing – Independent-Samples t Test
In Part I we compared the mean scores for men and women for the following variables.
- educ
- hrs1
A t test is used when you want to compare two groups. That means that your row variable must be a dichotomy consisting of only two categories. The variable sex is a dichotomy. It has only two categories – male (value 1) and female (value 2). But any variable can be made into a dichotomy by recoding. For example, the variable satfin (satisfaction with financial situation) has three categories – satisfied (value 1), more or less satisfied (value 2), and not at all satisfied (value 3). You could recode satfin to combine values 1 and 2 which would then give you a dichotomy (i.e., satisfied and not satisfied).
Click on MEANS in the menu bar at the top of SDA and enter the variables educ and hrs1 in the DEPENDENT box as you did in Part I. The SELECTION FILTER(S) box and the WEIGHT box should both be filled in. Be sure to click on OUTPUT OPTIONS and both check SRS STD ERRS and uncheck COMPLEX STD ERRS. Now we want to determine if the differences between men and women are statistically significant by carrying out the independent-samples t test. Click on OUTPUT OPTIONS and check the box for ANOVA STATS under OTHER OPTIONS. Finally, click RUN THE TABLE to carry out the procedure.
You’re probably wondering why we requested the ANOVA table. (By the way, ANOVA means Analysis of Variance.[1]) The t test is a special case of One-Way Analysis of Variance[2] when your independent variable is a dichotomy. In this special case, the F statistic in the Analysis of Variance table for education is the square of the t statistic. So to get t all you have to do is to take the square root of 0.342 which is 0.585. The degrees of freedom (df) is 2,535 which you can get from the ANOVA table. The P value is the probability that you would be wrong if you rejected the null hypothesis that there was no difference between the means for the population of all men and the population of all women[3].
Notice how we are going about this. We have a sample of adults in the United States (i.e., the 2014 GSS). We calculate the mean years of school completed by men and women in the sample who answered the question. But we want to test the hypothesis that the mean years of school completed by men and women in the population are different. We’re going to use our sample data to test a hypothesis about the population.
The hypothesis we want to test is that the mean years of school completed by men in the population is different than the mean years of school completed by women in the population. We’ll call this our research hypothesis. It’s what we expect to be true. But there is no way to prove the research hypothesis directly. So we’re going to use a method of indirect proof. We’re going to set up another hypothesis that says that the research hypothesis is not true and call this the null hypothesis. If we can’t reject the null hypothesis then we don’t have any evidence in support of the research hypothesis. You can see why this is called a method of indirect proof. We can’t prove the research hypothesis directly but if we can reject the null hypothesis then we have indirect evidence that supports the research hypothesis. We haven’t proven the research hypothesis, but we have support for this hypothesis.
Here are our two hypotheses.
- research hypothesis – the population mean for men minus the population mean for women does not equal 0. In other words, they are different from each other.
- null hypothesis – the population mean for men minus the population mean for women equals 0. In other words, they are not different from each other.
It’s the null hypothesis that we are going to test.
Now all we have to do is figure out how to use the t test to decide whether to reject or not reject the null hypothesis. Look again at the P value which is 0.5587 for the t test. That tells you that the probability of being wrong if you rejected the null hypothesis is just about .56 or 56 times out of one hundred. With odds like that, of course, we’re not going to reject the null hypothesis. A common rule is to reject the null hypothesis if the significance value is less than .05 or less than five out of one hundred.
Part IV – Now it’s Your Turn Again
In this part of the exercise you want to compare men and women to answer these two questions but this time you want to test the appropriate null hypotheses.
- Do men and women differ in the number of hours per day they have to relax?
- Do men and women differ in the number of hours per day they watch television?
Use the independent-sample t test to carry out this part of the exercise. What are the research and the null hypotheses? Do you reject or not reject the null hypotheses? Explain why.
Part V – What Does Independent Samples Mean?
Why do we call this t test the independent-samples t test? Independent samples are samples in which the composition of one sample does not influence the composition of the other sample. In this exercise we’re using the 2014 GSS which is a sample of adults in the United States. If we divide this sample into men and women we would have a sample of men and a sample of women and they would be independent samples. The individuals in one of the samples would not influence who is in the other sample.
Dependent samples are samples in which the composition of one sample does influence the composition of the other sample. For example, if we have a sample of married couples and divide that sample into two samples of men and women, then the men in one of the samples determines who the women are in the other sample. The composition of the samples is dependent on each other. SDA does not include a test for dependent samples.
[1] We’ll talk more about Analysis of Variance in exercise STAT8S_SDA.
[2] One-way just means that there is only one independent variable.
[3] Null means that it is a hypothesis of no difference. In other words, there is no difference between the means for men and for women. Notice that this refers to the mean of the population of all men and the mean of the population of all women. In other words, we are using our sample data to test a hypothesis about population values.


