Author: Ed Nelson
Department of Sociology M/S SS97
California State University, Fresno
Fresno, CA 93740
Email: ednelson@csufresno.edu
Note to the Instructor: This is the sixth in a series of 13 exercises that were written for an introductory research methods class. The first exercise focuses on the research design which is your plan of action that explains how you will try to answer your research questions. Exercises two through four focus on sampling, measurement, and data collection. The fifth exercise discusses hypotheses and hypothesis testing. The last eight exercises focus on data analysis. In these exercises we’re going to analyze data from one of the Monitoring the Future Surveys (i.e., the 2017 survey of high school seniors in the United States). This data set is part of the collection at the Inter-university Consortium for Political and Social Research at the University of Michigan. This data set is freely available to the public and you do not have to be a member of the Consortium to use it. We’re going to use SDA (Survey Documentation and Analysis) to analyze the data which is an online statistical package written by the Survey Methods Program at UC Berkeley and is available without cost wherever one has an internet connection. A weight variable is automatically applied to the data set so it better represents the population from which the sample was selected. You have permission to use this exercise and to revise it to fit your needs. Please send a copy of any revision to the author so I can see how people are using the exercises. Included with this exercise (as separate files) are more detailed notes to the instructors and the exercise itself. Please contact the author for additional information.
This page in MS Word (.docx) format is attached.
Goal of Exercise
The goals of this exercise are to provide an introduction to data analysis and specifically to discuss the different levels of analysis (univariate, bivariate, multivariate) and levels of measurement (nominal, ordinal, interval, and ratio).[1]
Part I—Introduction to Data Analysis
All research starts with one or more research questions. These are the questions that you want to answer in your research study. For example, you might want to find out why some people vote Democrat and others vote Republican or you might want to find out why some people don’t vote at all. Another question you might want to try to answer is why some favor same-sex marriage and others oppose it.
A research design is your plan of action. It lays out how you plan to go about answering your questions. The research design includes how you plan to select the cases for analysis (sampling), how you will measure concepts, how you plan to collect your data, and how you will analyze the data. In this exercise we’re going to discuss two important components of data analysis – levels of analysis (univariate, bivariate, and multivariate) and levels of measurement (nominal, ordinal, interval, and ratio). If your arrangement is sufficiently big and complex it might also be a fantastic idea to utilize Progressive Delivery -- it permits you to get and review different chapters of the homework assignment prior to the author completed working around the text completely, thereby allowing for a far greater amount of control compared to the customary arrangement. If you would like to keep your eye on the event, this can be the option for you. Another way it is possible to get involved in the planning of your custom made homework is that the usage of Samples support -- using its help you'll receive access to a number of newspapers written by your author previously. By analyzing their fashion and assessing their ability, you can choose whether that writer suits you or you need someone else to be delegated to the sequence into his stead. In general, place your order and then fill in all of your requirements and our hw helpmate authors will supply you immediate homework writing help in virtually any area.
The research study that we’ll be using in these exercises is the Monitoring the Future (MTF) Survey of high school seniors in the United States that has been conducted yearly since 1975. There is a website that will give you a lot of information about this study. Here’s a brief description from the website’s home page.
“Monitoring the Future is an ongoing study of the behaviors, attitudes, and values of American secondary school students, college students, and young adults. Each year, a total of approximately 50,000 8th, 10th and 12th grade students are surveyed (12th graders since 1975, and 8th and 10th graders since 1991). In addition, annual follow-up questionnaires are mailed to a sample of each graduating class for a number of years after their initial participation.”
A major focus of these surveys is students’ drug use. But the surveys include a lot more information than just drug use. The website describes the range of questions asked.
“Questions include drug use and views about drugs, delinquency and victimization, changing roles for women, confidence in social institutions, concerns about energy and ecology, and social and ethical attitudes.”
These are only a few of the areas that students are asked about. Other areas include, for example, their educational goals, religion, politics, the military, race, health, and background information including their family.
Part II – Levels of Analysis
Data analysis is always cumulative. It starts at the simplest level and then builds to more complex levels. Analysis is often described as univariate, bivariate, and multivariate.
Univariate or one-variable analysis focuses on single variables. For example, most data sets include age as a variable. Univariate analysis starts by looking at the frequency distribution for age. Frequency distributions tell us how many respondents are at each age. Measures of central tendency (e.g., mean, median, mode) provide us with a measure of the center of the distribution. Measures of dispersion (e.g., range, standard deviation, variance, index of qualitative variation) tell us how spread out the values are. Measures of skewness describe how much distributions deviate from a symmetrical, bell-shaped pattern. Measures of kurtosis tell us how peaked or flat distributions are. Graphs or charts (e.g., pie charts, bar graphs, line graphs) provide us with a visual picture of the distribution. It’s important to have an understanding of what each variable looks like before we begin looking at relationships between variables.
Bivariate or two-variable analysis focuses on pairs of variables. The goal is to discover the relationship between variables. For example, we might be interested in the relationship between age and voting behavior. Statistical techniques include crosstabulation, correlation, and regression among others.
Multivariate analysis focuses on sets of three or more variables. The goal is to extend our analysis to answer questions such as the following.
- Could the relationship between two variables be due to another variable?
- Why is there a relationship between two variables?
- Does the relationship vary for different types of individuals?
Statistical techniques used in multivariate analysis are an extension of crosstabulation, correlation, and regression.
Exercises seven through thirteen explore some of these statistical techniques. We’re not going to consider all these statistical tools but we are going to cover enough to give you the tools you need to begin data analysis. Before we begin we need to talk about levels of measurement – nominal, ordinal, interval, and ratio. It’s important that we choose the right statistical tools in our analysis. Our choice depends, in part, on the level of measurement of the variables we are using.
Part III – Levels of Measurement
We use concepts all the time. For example, religiosity is a concept which refers to the degree of attachment that individuals have to their religious preference. It’s different than religious preference which refers to the religion with which they identify. Some people say they are Lutheran; others say they are Roman Catholic; still others say they are Muslim; and others say they have no religious preference. Religiosity and religious preference are both concepts.
A concept is an abstract idea. So there are the abstract ideas of religiosity, religious preference, and many others. Since concepts are abstract ideas and not directly observable, we select measures or indicants of these concepts. Religiosity can be measured in a number of different ways – how often people attend church, how often they pray, and how important they say their religion is to them.
In these exercises we’re going to use the MTF Surveys of high school seniors in the United States that has been conducted yearly since 1975. Information about these surveys is archived at the Inter-university Consortium for Political and Social Research (ICPSR) located at the University of Michigan. You will need to get an account at ICPSR before you can use this data set. All accounts are free. To find out how to create an account, go to the appendix to these exercises called " Introduction to SDA". This introduction will also give you a brief overview of SDA.
MTF is an example of a social survey. The investigators selected a sample from the population of all high school seniors in the United States. This particular survey was conducted in 2017 and is a relatively large sample of a little less than 14,000 high school students. In a survey we ask respondents questions and use their answers as data for our analysis. The answers to these questions are used as measures of various concepts. In the language of survey research these measures are typically referred to as variables. Often we want to describe respondents in terms of social characteristics such as age, sex, and race. These are all variables in the MTF Survey. A weight variable is automatically applied to the data. This will weight the data so the sample better represents the population from which the sample was selected.
These measures are often classified in terms of their levels of measurement. S. S. Stevens described measures as falling into one of four categories – nominal, ordinal, interval, or ratio.[2] Here’s a brief description of each level.
A nominal measure is one in which objects (i.e. in our survey, these would be high school seniors) are sorted into a set of categories which are qualitatively different from each other. For example, we could classify individuals by their sex or race. Students are classified as being either male or female and also classified as being white, black, or Hispanic. There is also a separate category for students whose information is missing because they skipped that question. Our categories should be mutually exclusive and exhaustive. Mutually exclusive means that every individual can be sorted into one and only one category. Exhaustive means that every individual can be sorted into a category.
The categories in a nominal level measure have no inherent order to them. This means that it wouldn’t matter how we ordered the categories. They could be arranged in any number of different ways. Run FREQUENCIES in SDA for the variable V2151 which is the variable name for race so you can see the frequency distribution for a nominal level variable. To run the frequency distribution, enter the variable name, V2151, in the ROW box. Your screen should look like Figure 6-1. Then click on RUN THE TABLE at the bottom. Notice that the WEIGHT box is filled in for you. This will weight the data so the sample better represents the population from which the sample was selected.
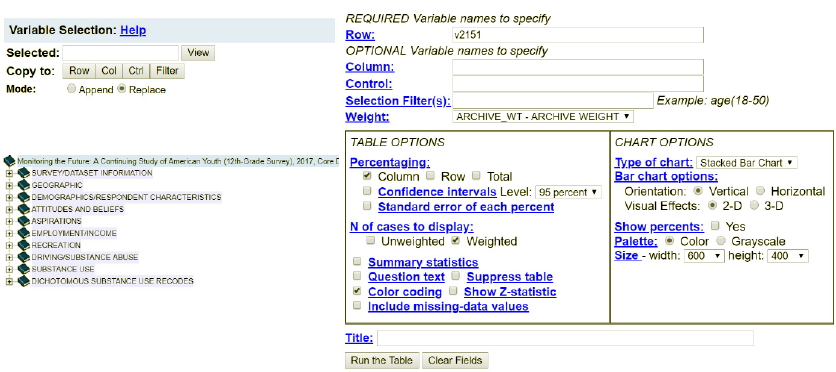
Figure 6-1
SDA will display the output in a separate window which should look like Figure 6-2. In this distribution the categories are black, white, and Hispanic. But they could also be ordered as Hispanic, white, black or in still other ways. It doesn’t matter how you order the categories in a nominal variable.
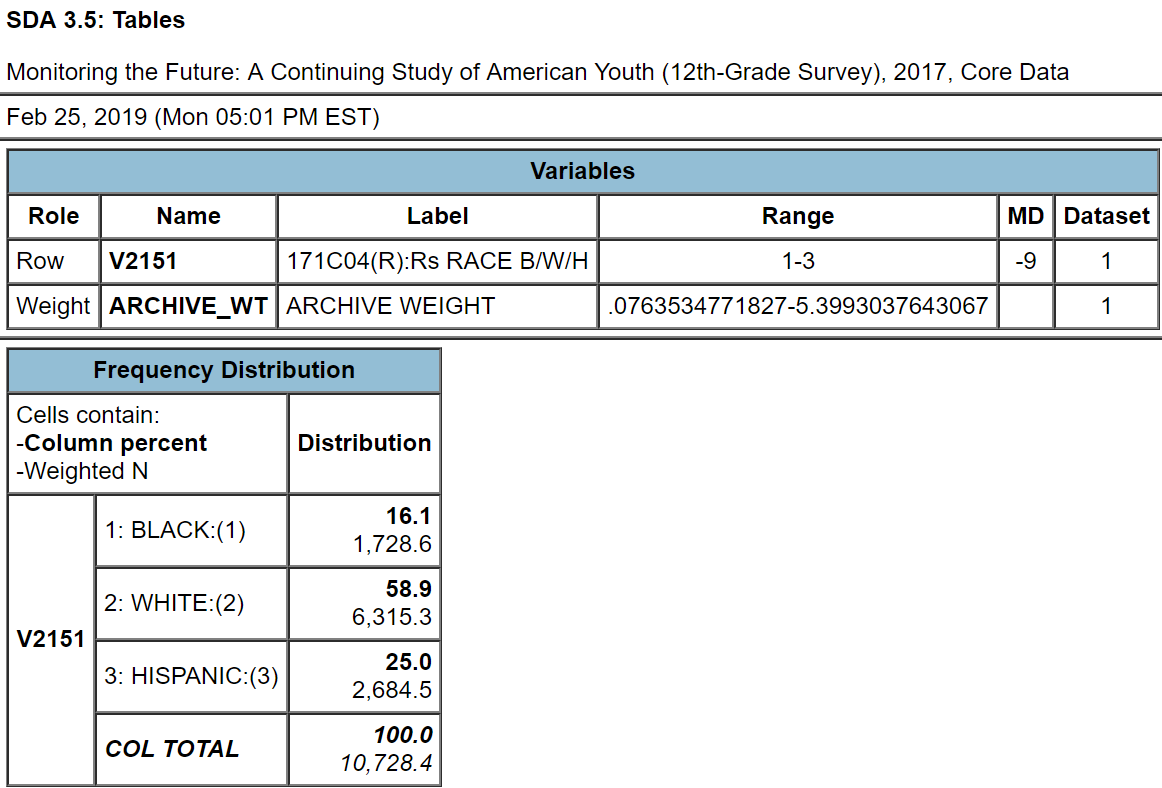
Figure 6-2
An ordinal measure is a nominal measure in which the categories are ordered from low to high or from high to low. Two of the questions in the survey asked about the highest level of schooling for both the respondent’s father and mother. Some parents attended only grade school; others attended high school but did not complete it; others graduated from high school but didn’t go on to college. Still other individuals attended college but did not graduate; others graduated from college; and still others completed their bachelor’s degree and went on to graduate work. These categories are ordered from low to high.
But notice that while the categories are ordered they lack an equal unit of measurement. That means, for example, that the differences between categories are not necessarily equal. Run FREQUENCIES in SDA for V2163 and V2164. Look at the categories. MTF assigned values (i.e., numbers) to these categories in the following way:
- 1 = grade school,
- 2 = some high school,
- 3 = high school graduate,
- 4 = some college,
- 5 = college graduate, and
- 6 = graduate school.
The difference in education between the first two categories is not the same as the difference between the last two categories. We might think they are because 1 minus 2 is equal to 5 minus 6 but this is misleading. These aren’t really numbers. They’re just symbols that we have used to represent these categories. We could just as well have labeled them a, b, c, d, e, and f. They don’t have the properties of real numbers. They can’t be added, subtracted, multiplied, and divided. All we can say is that b is greater than a and that c is greater than b and so on.
An interval measure is an ordinal measure with equal units of measurement. For example, consider temperature measured in degrees Fahrenheit. Now we have equal units of measurement – degrees Fahrenheit. The difference between 20 degrees and 40 degrees is the same as the difference between 70 degrees and 90 degrees. Now the numbers have the properties of real numbers and we can add them and subtract them. But notice one thing about the Fahrenheit scale. There is no absolute zero point. There can be both positive and negative temperatures. That means that we can’t compare values by taking their ratios. For example, we can’t divide 80 degrees Fahrenheit by 40 degrees and conclude that 80 is twice as hot as 40. To do that we would need a measure with an absolute zero point.[3]
A ratio measure is an interval measure with an absolute zero point. For example, consider the number of siblings. This variable has an absolute zero point and all the properties of nominal, ordinal, and interval measures and therefore is a ratio variable.
Notice that level of measurement is itself ordinal since it is ordered from low (nominal) to high (ratio). It’s what we call a cumulative scale. Each level of measurement adds something to the previous level.
Why is level of measurement important? One of the things that helps us decide which statistic to use is the level of measurement of the variable(s). For example, we might want to describe the central tendency of a distribution. If the variable was nominal, we would use the mode. If it was ordinal, we could use the mode or the median. If it was interval or ratio, we could use the mode or median or mean. Central tendency will be the focus of exercise 7RM.
Part IV – Now It’s Your Turn
Run FREQUENCIES in SDA for the following variables.
- V2152 – where the respondent grew up
- V2166 – political party preference
- V2167 – political views
- V2169 – how often respondent attends religious services
- V2178 – number of days of school in the last four weeks that respondent skipped or cut
- V2108 – number of times in the last two weeks that respondent had five or more drinks in a row
- V2116 – number of times that respondent used marijuana or hashish in the last twelve months
For some of these variables, you will want to see the wording of the question to know what the response categories mean. To do that find the question in the mini-codebook on the left and click on that variable. That will insert that variable in the “Variable Selection” box. All you have to do is click on the “View” button and the question wording will be displayed. See the “Introduction to SDA” in the appendix for more instructions on how to do this.
For each variable, decide which level of measurement it represents and write a sentence or two indicating why you think it is that level. Sometimes respondents fail to answer the question either because they don’t know the answer or they refuse. These responses need to be designated as missing values. Indicate in your answer for each variable which value(s) should be designated as missing values. Do not take them into account when you decide on the level of measurement for that variable.
[1] In these exercises we’re going to focus on survey research.
[2] Stanley Smith Stevens, 1946, “On the Theory of Scales of Measurement,” Science 103 (2684), pp. 677-680.
[3] Notice that we didn’t offer a social science example of an interval measure. That’s because there aren’t many interval variables in the social sciences. It’s easier to think of examples in business. Profit is an interval measure because it lacks an absolute zero point. Profit can be either positive or negative.


