Many of the problems that social scientists study are dynamic in character. A sociologist interested in the process of friendship formation would want to look at the way friendship dyads are formed over time. A political scientist interested in voting behavior would look at the ways in which people make up their minds for whom to vote. An economist studying consumer optimism might want to trace consumer sentiment over a period of years and see how that relates to other changes in the economy and the society.
A survey that looks at a cross-section of a group at one point in time (often called a cross-sectional survey) is not well suited to a study of dynamic processes. The political scientist interested in voting behavior might include questions that asked respondents who they had intended to vote for at the beginning of the campaign and who they plan to vote for now. This would allow an analysis of how voting decisions have changed over the campaign, but at a severe cost. The respondents' memory of who they preferred at the beginning of the campaign might be influenced by who they prefer later. We need some way to adapt cross-sectional surveys to the study of dynamic problems in which the focus is on change over time.
Cross-sectional studies focus on a group at one point in time. The Census is a good example of a cross-sectional study. The 1990 Census describes the U.S. population at one point in time -- April, 1990. Longitudinal studies focus on the group at two or more points in time. We're going to look at three types of longitudinal studies -- the trend study, the panel study, and the cohort study.
TREND STUDIES
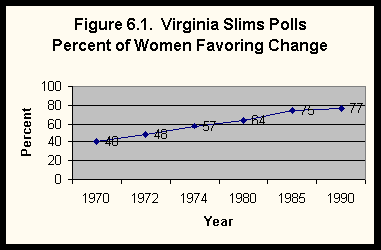
Trend studies use cross-sections at two or more points in time to examine change over time. The Virginia Slims Opinion Poll asked various questions about women at six points in time (The Roper Center 1990). The first poll was conducted in 1970, and it was repeated in 1972, 1974, 1980, 1985, and 1990. The Virginia Slims polls are national probability samples of all adults living in the United States. These six cross-sectional surveys can be compared to trace changes in opinions and attitudes about women from 1970 to 1990.
Figure 6.1 shows the percent of women who favor efforts to strengthen and change women's status in society. The percent who favor such efforts has increased steadily from 1970, while the percent who oppose has decreased.
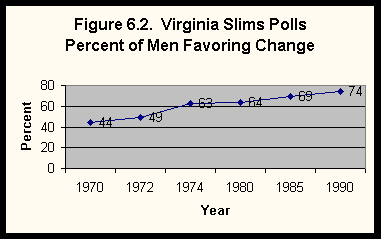
Figure 6.2 shows the same information for men. The pattern is the same for men as it is for women, but the percent of women favoring change is now larger (77%) than the percent of men (74%).
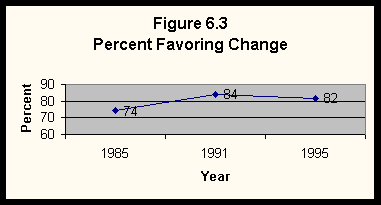
In 1985, 1991, and 1995, the Field Poll asked virtually the same question of a sample of California residents age 18 and over. Figure 6.3 shows the percent of respondents who favor such efforts. We got these percentages by crosstabulating the dependent variable (i.e., favor or oppose efforts) by time (i.e., year). Clearly the changes in opinion in California are similar to the national patterns.
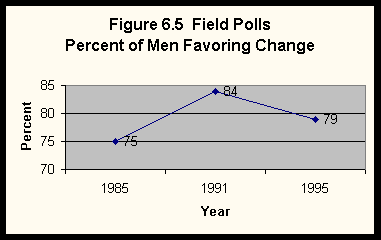
The Virginia Slims Polls showed the percentages separately for women and men. We can get this information for the Field Polls by crosstabulating the dependent variable by time and holding sex constant. This will give us two sets of figures, one for women and one for men. Figure 6.4 shows the percent of women who favor changes in women's roles, while Figure 6.5 shows the same for men. Notice that the percentages increased for women from 72.1% in 1985 to 83.7% in 1991 and then to 85.1% in 1995, while the percentages for men increased from 75.0% in 1985 to 83.7% in 1991 and then decreased to 79.3% in 1995.
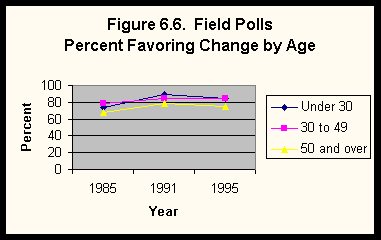
Let's look at the Field Polls for another example of change from 1985 to 1995. Figure 6.6 shows the percent who favor strengthening the status of women for three age groups--those under 30, those 30 to 49, and those 50 and over. We can learn several things from this table. First, the percent who favor such change increased in all age groups from 1985 to 1991 and then stayed about the same in 1995. Second, in all time periods, those 50 and over are least likely to favor such change.
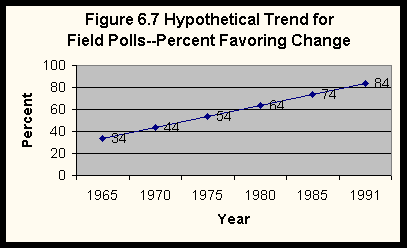
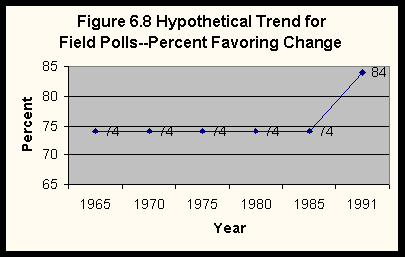
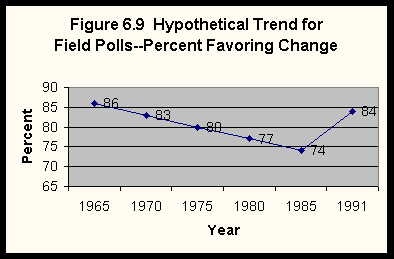
You might have noticed one difference between the Virginia Slims example and the Field Poll example. The Virginia Slims data are based on six time periods, while the Field Poll data are based on three time periods. Does this make any difference? Figure 6.7 shows the percent who favor efforts to strengthen the status of women in 1985 and 1991 in the Field Poll. Clearly the percent who favor increased from 1985 to 1991. Let's imagine what the pattern might look like if we had data from four time periods prior to 1985. Figure 6.7 shows a long-term trend of increasing support. Figure 6.8 shows a long-term trend of little change with an increase from 1985 to 1991. Figure 6.9 shows a long-term trend of decreasing support with a reversal in this trend from 1985 to 1991. Without more time periods it is very difficult to determine what the long-term trend actually looks like. The 1995 Field Poll indicates that there has been little change from 1991 to 1995. This example suggests that many time periods are better than few time periods. However, remember that every trend analysis must start with two points in time and build from that to a longer series.
Figure 6.8 indicates that there was a ten percentage point increase from 1985 to 1991 in the percent of respondents who favor strengthening the status of women. Was this produced by the shift of some individuals who opposed such changes in 1985 (or had no opinion) to a position that favors these changes in 1991? While it might seem tempting to accept this interpretation, it is not necessarily true. Table 6.1 shows a hypothetical example that is consistent with this interpretation. All of the individuals who favored change in 1985 also favor change in 1991. However, some of those who opposed change in 1985 now favor change in 1991 (n = 26), while more have shifted to a position of don't know (n = 76). Table 6.2 shows an example in which there has been a considerable shift in opinion in both directions--from oppose to favor and from favor to oppose. A considerable number of those who favored change in 1985 oppose change in 1991 (n = 100), while many of those who opposed change in 1985 now favor change (n = 115) or say they don't know (n = 87). Unfortunately, in a trend study we cannot choose between these alternatives. The most we can do in a trend study is to describe net changes between time periods. If we want to describe shifts from favor to oppose or from oppose to favor, then we need a different type of data called panel data.
PANEL STUDIES
Panel studies describe information about the same cases at two or more points in time. In a trend study we compare sample surveys describing the same population at two or more points in time. These samples consist of different cases. In a panel study we compare the same cases over time. If the Field Poll had been able to reinterview the same individuals in 1991 and 1995 that were interviewed in 1985, then it would have been a panel study. The advantage of panel studies is that we can choose between alternatives such as those presented in Tables 6.1 and 6.2. Panel data allow us to go beyond describing net changes between time periods. Panel data allow us to describe the types of shifts (e.g., from favor to oppose or from oppose to favor) that occur between time periods. We can also begin looking for factors that explain why some people change in one direction, while other individuals change in another direction, and still others do not change at all.
Table 6.1 -- Hypothetical Example Showing Opinion Shifts from 1985 to 1991 1985 1991 Favor Oppose Don't Know Total
Table 6.2 -- Hypothetical Example Showing Opinion Shifts from 1985 to 1991 1985 1991 Favor Oppose Don't Know Total
However, there are also problems with panel data. It is rare that all the cases are available in later time periods. This is called panel mortality. When the case is the individual, this may be because some individuals are not alive at a later point in time. However, all panel mortality may not be due to the death of respondents. Some respondents who cooperated initially may choose not to cooperate later. If particular types of individuals choose not to cooperate at a later point in time, then bias is introduced. For example, if low income respondents choose not to cooperate at a later point in time and if low income respondents are less likely to favor efforts to change the status of women, then part of the shift in opinion might be due to panel mortality.Another problem with panel data is reactivity. If we ask people questions about the status of women at two or more points in time, the questioning process itself might produce opinion shifts. Perhaps the act of asking people about the status of women makes them more sensitive to women's issues. This increased sensitivity might mean they are more likely to favor or to oppose changes in the status of women during later surveys. We call this reactivity because the respondents are reacting to the initial questioning.
COHORT STUDIES
Table 6.3 shows the percent who disagree that "women should take care of running their homes and leave running the country to men" by age for three of the General Social Surveys (1975, 1983, 1991). The General Social Survey is a national probability sample of all adults living in the United States (Davis and Smith 1992). This table can be analyzed in several ways.
Table 6.3. Percent of Respondents Who Disagreed that "Women should take care of their homes and leave running the country up to men."* Age 1975 (n) 1983 (n) 1991 (n) 18-25 78.5 (251) 87.2 (203) 85.0 (120) 26-33 75.6 (258) 84.7 (360) 90.1 (172) 34-41 67.5 (194) 83.0 (241) 91.5 (201) 42-49 68.3 (183) 81.4 (177) 86.5 (133) 50-57 58.4 (173) 76.3 (160) 78.0 (82) 58-65 56.1 (155) 66.5 (167) 80.2 (101) 66-73 39.0 (136) 57.6 (125) 58.0 (81) 74+ 42.9 (91) 47.5 (99) 48.9 (90) Total 64.4 (1441) 76.9 (1532) 80.8 (980) * The data are from the General Social Survey. The values inside the parentheses are the number of cases on which the percentages are based (i.e., the bases).
First, we can compare opinions in the three time periods. We could compare the percent who disagree for each time period. This would show that there has been growing disagreement with this statement (64.4% of the total sample disagreed in 1975, 76.9% in 1983, and 80.8% in 1991). We could also compare the percent who disagree within each age group. For example, we could compare those age 34 to 41 in each of the three time periods (67.5% of those 34 to 41 disagree in 1975, 83.0% in 1983, and 91.5% in 1991) and repeat this for each of the age categories. This would involve comparing percentages across each row and this would show that there has been increasing disagreement even when we hold age constant.Second, we could compare age categories within each time period. This would involve comparing percentages down within columns. This would show that the older respondents are less likely to disagree in each time period. In each of the three time periods, those age 66 to 73 and those 74 and over are considerably less likely to disagree than the younger respondents. (Note: even they increase over time--42.9% in 1975, 47.5% in 1983, 48.9% in 1991.)
Third, we could compare birth cohorts. Groups of people born within the same time period are called birth cohorts. The time period can be defined in any way that is appropriate for your analysis. Here we are using eight-year periods--all the people born within an eight-year period belong to the same birth cohort. Those who are 18 to 25 in 1975 would be 26 to 33 in 1983 and 34 to 41 in 1991. We could look at each of the birth cohorts in this table separately. This would involve comparing percentages along the diagonals running from the upper left part of the table to the lower right part. For example, for the birth cohort who was 18 to 25 in 1975, the percentages would be 78.5 in 1975, 84.7 in 1983, and 91.5 in 1991. In general, the cohorts are more likely to disagree with the statement in each successive time period. We could also compare other birth cohorts. The pattern described above is particularly noticeable for the four younger cohorts (i.e., those 18 to 25, 26 to 33, 34 to 41, and 42 to 49 in 1975).
Cohort studies follow one or more cohorts (usually at least two) over a period of time. Cohort studies are usually based on two or more cross-sectional studies. In the example above, we have used three cross-sectional surveys (1975, 1983, 1991) and arranged the data so that we can compare birth cohorts.
SUMMARY
The purpose of this chapter has been to start you thinking about questions related to change over time. The analysis of such questions require longitudinal data. We have described three types of longitudinal studies -- the trend study, the panel study, and the cohort study. The exercises in the next chapter will give you some practice in exploring changes in opinions on women's issues by using the Field Polls conducted in 1985, 1991, and 1995.
Last Modified 15 August 1998